Ideální plyn

Ideální plyn je zjednodušeným modelem reálného plynu. Umožňuje poměrně snadno určit chování plynu nebo směsi plynů. Pro chování ideálního plynu platí následující pravidla:

Částice plynu považujeme za hmotné body, které nemají svůj objem. Plyn lze tedy stlačit na nulový objem.
Částice spolu neinteragují, pouze se srážejí.
Při srážkách se částice plynu chovají jako dokonale pružná tělesa. Při srážkách nedochází k výměně energie mezi částicemi.

Obsah

1 mol ideálního plynu při teplotě 25 °C a tlaku 101,325 kPa zaujímá objem 22,414 dm³ (molární objem, V_m).

$$n=\frac{V}{V_m}$$

Plyn	Objem 1 molu [dm³]
Ideální plyn	22,414
Ar	22,09
CO₂	22,26
N₂	22,40
O₂	22,40
H₂	22,43

Stavová rovnice ideálního plynu

Stavová rovnice popisuje vztah mezi tlakem, objemem a teplotou plynu.

$$pV = nRT = \frac{m}{MRT}$$ $$\rho = \frac{pM}{RT}$$ $$M = \frac{\rho RT}{p} = \frac{RT}{V_m}$$

R = 8,314 4621(75) J.K^-1.mol^-1; molární plynová konstanta

Pro změny stavu plynu platí:

$$\frac{p_1V_1}{n_1T_1} = \frac{p_2V_2}{n_2T_2}$$

Molární objem

Ze stavové rovnice můžeme vypočítat molární objem. Jeho hodnota pochopitelně závisí na teplotě a tlaku, při 0 °C a tlaku 101 325 Pa je molární objem:

$$V_m = \frac{nRT}{p} = \frac{1\ .\ 8,314\ .\ 273,15}{101\ 325} = 22,414\ dm^3.mol^{-1}$$

Při tlaku 100 kPa, který je IUPACem stanovený jako standardní tlak je pak molární objem 22,711 dm³.mol^-1.

$$V_m = \frac{nRT}{p} = \frac{1\ .\ 8,314\ .\ 273,15}{100\ 000} = 22,711\ dm^3.mol^{-1}$$

Standardní podmínky pro plyny

IUPAC definuje standardní podmínky pro plyny jako 0 °C a 100 kPa. Dříve používaný tlak 101 325 Pa (1 atmosféra) už není doporučovaný.

Boyleův zákon

Součin tlaku a objemu plynu je za izotermických podmínek konstantní. Pokud dojde ke zvýšení tlaku, musí se úměrně zmenšit objem a naopak.

p.V = konst.

p₁.V₁ = p₂.V₂

Daltonův zákon

Celkový tlak směsi plynů je roven součtu parciálních tlaků všech složek směsi.

$$p_{celk} = \displaystyle\sum_{i=0}^{n} p_i$$

Parciální tlak

Tlak komponenty ve směsi. Složky směsi ideálních plynů se v nádobě chovají, jako by tam byly samy.

Molární zlomek

$$X_i = \frac{n_i}{\sum n}$$

Parciální tlak plynu ve směsi vypočítáme jako součin celkového tlaku v systému a molárního zlomku plynu:

$$p_i\ =\ p\ .\ X_i$$

Děje v plynech

Pokud během děje dochází ke změně všech tří stavových veličin (p, V, T) počítáme se stavovou rovnicí, jak je uvedeno výše. Pokud je jedna z veličin konstantní, můžeme si výpočet zjednodušit.

Izochorický děj

Objem plynu je během děje konstantní. Ze stavové rovnice ideálního plynu vyplývá, že:

$$p = konst . T$$

$$\frac{p}{T} = konst.$$

$$\frac{p_1}{T_1} = \frac{p_2}{T_2}$$

Tlak plynu je tedy přímo úměrný teplotě plynu.

Příkladem izochorického děje je např. ohřev vzduchu v pneumatice při jízdě. Pokud je při teplotě 20 °C tlak v pneumatice 200 kPa, můžeme snad spočítat tlak při teplotě 60 °C, což odpovídá pneumatice zahřáté jízdou v horkém létě.

$$p_2 = \frac{p_1 . T_2}{T_1} = \frac{200 000 . 333,15}{293,15} = 227 290 Pa$$

Tlak tedy během jízdy vzroste přibližně na 227 kPa, čili o více než 14 %.

Izobarický děj

Tlak je během děje konstantní. Ze stavové rovnice ideálního plynu vyplývá, že:

$$V = konst . T$$

$$\frac{V}{T} = konst.$$

$$\frac{V_1}{T_1} = \frac{V_2}{T_2}$$

Objem plynu je tedy přímo úměrný teplotě plynu.

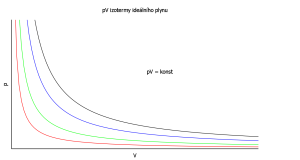
Izotermický děj

Teplota je během děje konstantní. Ze stavové rovnice ideálního plynu vyplývá, že:

$$p.V = konst.$$

$$p_1.V_1 = p_2.V_2$$

Součin tlaku a objemu je za konstantní teploty během všech pochodů konstantní (viz Boyleův zákon).

Reálný plyn

Chování reálného plynu popisuje van der Waalsova stavová rovnice:

$$(p+\frac{an^2}{V^2})(V – nb) = nRT$$

Konstanty a a b najdeme v tabulkách. Člen $\frac{an^2}{V^2}$ je korekce na interakce molekul a člen nb je korekce na vlastní objem částic.

Plyn	a $[\frac{m^2 Pa}{mol^2}]$	b $[10^{-6} \frac{m^3}{mol}]$
Chlor	0,658	56,2
Helium	0,0035	34,1
Krypton	0,235	39,8
Kyslík	0,138	31,8
Methan	0,228	42,8
Vodík	0,0247	26,6

Další příklady najdete zde.