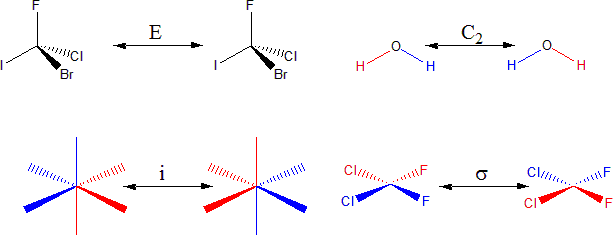
Správné určení symetrie molekuly je velmi důležité pro odhad reaktivity i pro určování jejich spektroskopických vlastností. Symetrický je každý prostorový objekt, který lze pomocí některé operace transformovat tak, aby jeho nový stav byl nerozlišitelný od výchozího.
Operace symetrie
Operace symetrie je transformace, pomocí kterou převádíme objekt z jednoho stavu do druhého, přičemž oba stavy jsou nerozlišitelné. Body objektu, které během transformace nezmění polohu leží v tzv. prvku symetrie. Výčet operací a prvků symetrie, které nacházíme u molekul je v tabulce dole:
| Operace symetrie | Prvek symetrie | Označení |
|---|---|---|
| Identita | Celý objekt | E |
| Rotace | Rotační osa | Cn |
| Zrcadlení | Zrcadlová rovina | σ |
| Inverze | Střed symetrie | i |
| Rotačně-reflexní operace (nevlastní rotace) | Rotačně-reflexní osa | Sn |
Identita
Objekt zůstává po provedení této operace nezměněn, všechny body jsou na původních místech. Tuto operaci symetrie mají všechny objekty.
Rotace
S objektem rotujeme o úhel \(\frac{2\pi}{n}\), kde n je četnost. Četnost se uvádí u symbolu rotace jako dolní index, např. dvojčetná osa se označuje C2, rotace podél dvojčetné osy otočí objekt o π, čili 180°. Podle konvence provádíme rotaci vždy ve směru hodinových ručiček.
Speciální osou je jednočetná rotační osa, C1, která otočí objekt o 360°, což znamená, že všechny body zůstávají na původních místech. Jedná se tedy o identitu.
Zrcadlení
Zrcadlová rovina se chová jako zrcadlo, tzn. přenáší body z jedné poloroviny do druhé a naopak. U molekul rozlišujeme, podle orientace vůči hlavní rotační ose, rovinu horizontální (σh), vertikální (σv) a diagonální (σd). Zrcadlení v rovině je operace, která je vůči sobě inverzní, takže pro její mocniny platí:
σ2n = E
σ2n+1 = σ
To znamená, že pokud zrcadlení provedeme dvakrát (čtyřikrát, šestkrát, …), získáme stejný výsledek, jako po aplikovaní identity, pokud ho provedeme třikrát (pětkrát, sedmkrát, …) je výsledek stejný, jako po prvním provedení této operace.
Inverze
V případě inverze, neboli zrcadlení přes střed symetrie, je prvkem symetrie jediný bod. Každý atom molekuly můžeme invertovat tak, že myšleně vedeme přímku přes atom a střed symetrie a přeneseme ho do druhé části přímky ve stejné vzdálenosti od středu, jako byl původní atom. Molekuly, které mají střed symetrie označujeme jako centrosymetrické, jde hlavně o lineární, čtvercové a oktaedrické molekuly. Centrosymetrické molekuly nemají dipólový moment.
Rotačně-reflexní operace
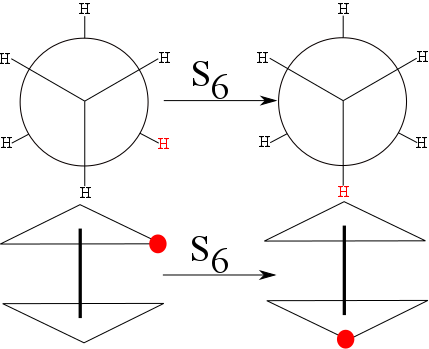
Operace složená z rotace kolem osy a zrcadlení v rovině kolmé k této ose. Značí se Sn. Při provádění této operace nezáleží na pořadí provádění jednotlivých kroků.
Příkladem nevlastní rotace je např. molekula ethanu ve střídavé konformaci, kde můžeme najít rotačně-reflexní osu S6. Tzn. že rotujeme okolo vazby C-C o 60° a poté provedeme zrcadlení v rovině kolmé na vazbu C-C a procházející jejím středem.
Bodové grupy symetrie
Množina všech operací symetrie dané molekuly se označuje jako grupa. Tyto grupy se označují jako bodové, protože během libovolné operace symetrie zůstává alespoň jeden bod beze změny. Bodové grupy symetrie se označují Schönfliesovou symbolikou.
V odkazech najdete link na tabulky charakterů jednotlivých bodových grup symetrie, v těchto tabulkách jsou obsaženy detailní informace o jednotlivých grupách.
Bodové grupy C1, Ci, Cs
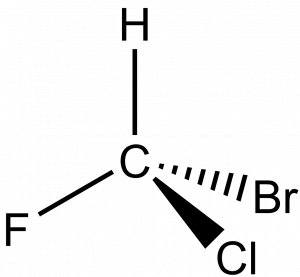
Bodová grupa symetrie C1 obsahuje jediný prvek symetrie, identitu E = C1. Příkladem je třeba tetraedrická molekula CHFClBr.
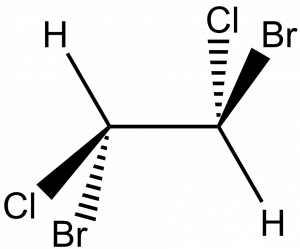
Bodová grupa symetrie Ci obsahuje dva prvky symetrie, identitu (E) a střed souměrnosti (i).
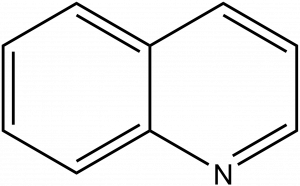
Bodová grupa symetrie Cs obsahuje dva prvky symetrie, identitu (E) a rovinu zrcadlení (σ). Příkladem jsou planární molekuly typu chinolin, které nemají rotační symetrii.
Bodové grupy Cn, Cnv a Cnh
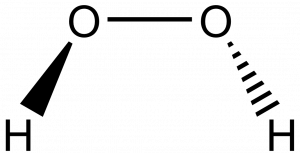
Bodové grupy symetrie Cn obsahuje identitu a rotační osu s četností n. Příkladem molekuly spadající do grupy C2 je peroxid vodíku.
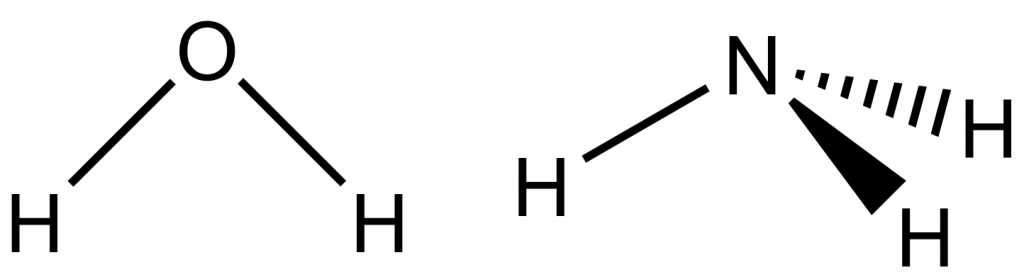
Bodové grupy symetrie Cnv obsahují identitu, rotační osu s četností n a n zrcadlových rovin. Příkladem bodové grupy C2v je molekula vody, tak obsahuje dvojčetnou rotační osu a dvě zrcadlové roviny. Molekula amoniaku má trojčetnou rotační osu a tři zrcadlové roviny (prochází každou vazbou N-H a půlí úhel HNH zbylých dvou vazeb), patří tedy do bodové grupy C3v.
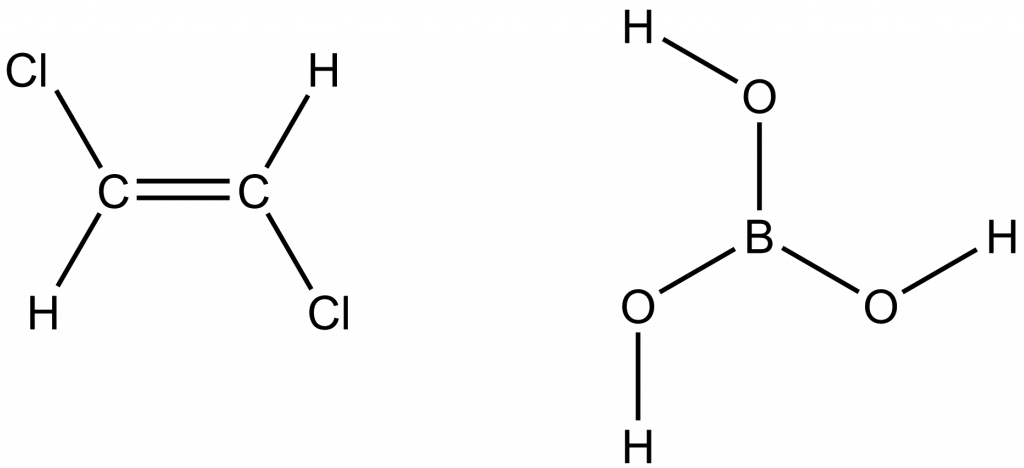
Bodové grupy symetrie Cnh obsahují identitu, rotační osu s četností n a horizontální zrcadlovou rovinu. V případě sudého n mají tyto grupy ještě střed symetrie. Příkladem molekuly patřící do grupy C2h je trans-1,2-dichlorethen, do grupy C3h patří např. kyselina boritá.
Bodové grupy Dn, Dnh, Dnd
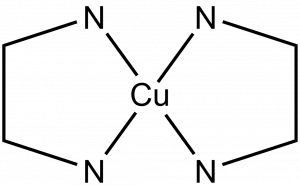
Obecně mají bodové grupy Dn n-četnou rotační osu a n dvoučetných os, kolmých na tuto osu. Grupa D1 je ekvivalentní grupě C2, obsahuje identitu a dvoučetnou rotační osu. Příkladem molekuly se symetrií D2 je bis(ethylendiamin)měďnatý komplex, který má tři dvoučetné, navzájem kolmé rotační osy procházející měďnatým iontem.
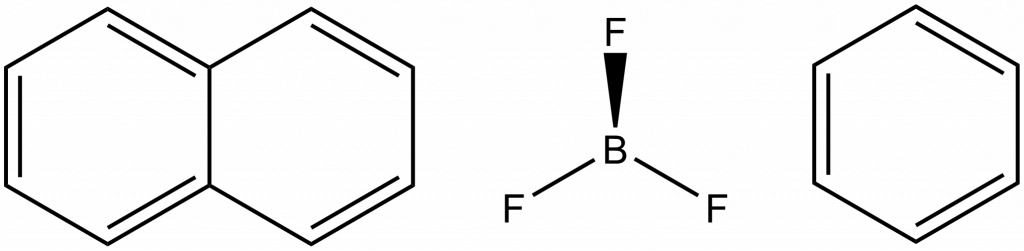
Bodové grupy Dnh obsahují hlavní osu o četnosti n, n dvoučetných os a horizontální rovinu symetrie. Pro sudé hodnoty n obsahuje i střed symetrie. Příkladem D2h je naftalen, D3h molekula BF3 a molekula benzenu je příkladem symetrie D6h.
Dvouatomové molekuly prvků, např. N2, O2 nebo Cl2 mají symetrii D∞h, takže mají nekonečný počet dvoučetných rotačních os procházejících středem spojnice atomů, hlavní osu o nekonečné četnosti procházející spojnicí atomů.
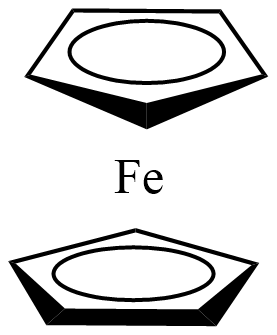
Bodové grupy Dnd obsahují hlavní osu o četnosti n, n kolmých dvoučetných os a n dihedrálních rovin symetrie σd. Příkladem může být ferrocen, který ve střídavé konformaci patří do bodové grupy symetrie D5d.
Kubické grupy
Do kubických grup patří molekuly mající více než jednu osu s četností vyšší než dvě.
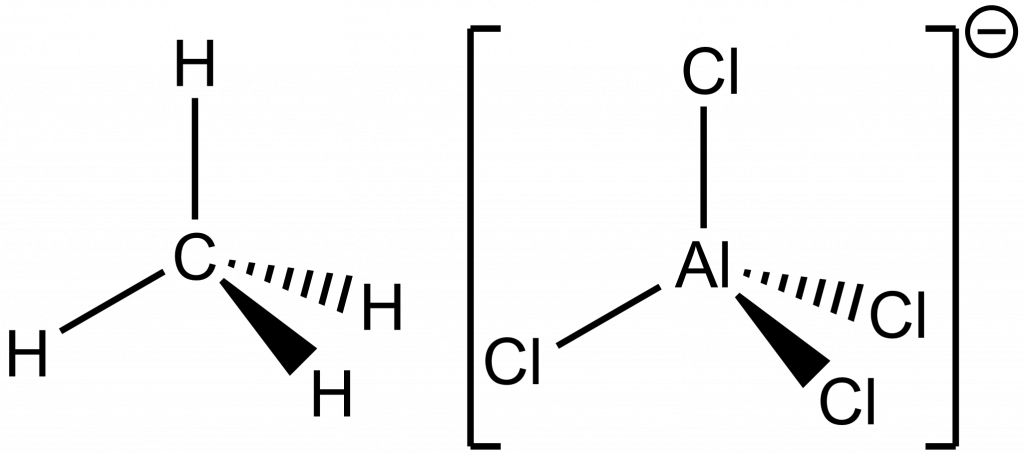
Tetraedrická grupa Td obsahuje kromě identity čtyři trojčetné osy, tři dvojčetné osy a šest diagonálních rovin symetrie. Do této grupy patří např. methan nebo tetrachloohlinitanový anion.
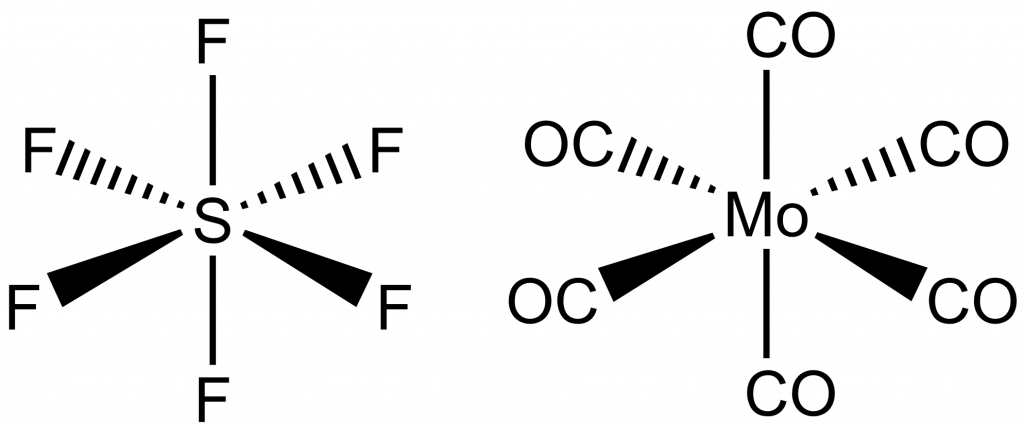
Oktaedrické molekuly patří do grupy Oh, která obsahuje identitu, střed symetrie a mnoho rotačních os i rovin souměrnosti. Do této grupy patří např. fluorid sírový nebo hexakarbonyl molybdenu.
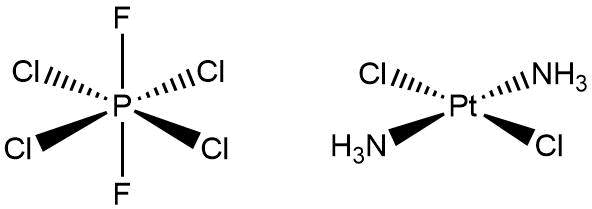
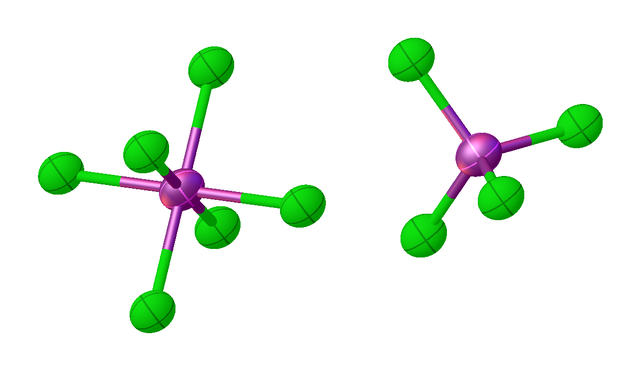
Oktaedrickou i tetraedrickou geometrii zároveň můžeme najít v koncentrovanějších roztocích chloridu fosforečného, který tvoří komplex [PCl6][PCl4].
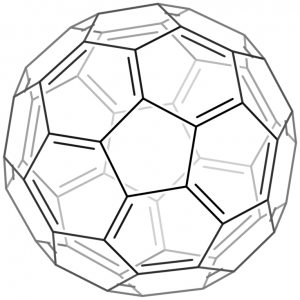
Molekuly s tvarem ikosaedru patří do grupy Ih, jde např. o fulleren C60 nebo jednotku elementárního boru B12.
Úplná rotační grupa
Tato grupa se skládá z nekonečného počtu os rotací se všemi možnými hodnotami četnosti, středu symetrie a nekonečného počtu zrcadlových rovin procházejících středem symetrie.
Odkazy
- Symmetry
- Symmetry around a Point in the Plane
- Character Tables for Point Groups used in Chemistry
- Symmetry@Otterbein – pěkný web, kde si můžete názorně zobrazit operace symetrie s jednotlivými molekulami
Další kapitoly
- České chemické názvosloví
- Platné číslice a měření
- Základní chemické zákony
- Důležité veličiny a vztahy v chemii
- Výpočet stechiometrického vzorce
- Chemické rovnice a stechiometrické výpočty
- Koncentrace roztoků
- Rozpustnost, součin rozpustnosti
- Stavba atomu
- Periodická tabulka prvků a periodicita vlastností
- Chemická vazba
- VSEPR
- Komplexní sloučeniny
- Magnetické vlastnosti látek
- Termodynamika
- Chemická rovnováha
- Skupenské stavy látek
- Fázové rovnováhy
- Teorie kyselin a zásad
- pH, aktivita roztoku
- Elektrochemie
- Symetrie molekul
- Laboratorní technika
- Lineární regrese
- Jednotky tlaku
- Jednotky teploty
- Mohsova stupnice tvrdosti minerálů
- Odkazy
- Prezentace k semináři z obecné chemie