Termodynamika – Web o chemii, elektronice a programování

Obsah

Termodynamika se zabývá procesy a vlastnostmi látek spojenými s teplem a teplotními přeměnami. Nezabývá se mechanismem ani rychlostí přeměny, umožňuje předpovědět směr reakce a její samovolnost a rozsah.

Důležité pojmy

Extenzivní veličiny – závisí na příspěvcích od jednotlivých částí soustavy, jsou aditivní – hmotnost, elektrický náboj, látkové množství, …
Intenzivní veličiny – nejsou aditivní – teplota, tlak, viskozita, koncentrace, hustota, …
Stav systému – je popsán intenzivními veličinami (T, p, c)
Stavová funkce – fyzikální charakteristika, jejíž hodnota závisí na stavu soustavy
Izolovaný systém – nevyměňuje s okolím ani energii, ani hmotu
Uzavřený systém – vyměňuje s okolím energii, ale ne hmotu
Otevřený systém – vyměňuje s okolím energii i hmotu
Teplota – pravděpodobnostní veličina, popisuje makroskopické systémy
Teplo – část vnitřní energie

Termodynamické zákony

Nultý

Jsou-li dvě a více těles v termodynamické rovnováze s tělesem dalším, pak jsou všechna tato tělesa v rovnováze

První

Celkové množství energie (všech druhů) izolované soustavy zůstává zachováno

Druhý

Teplo nemůže při styku dvou těles různých teplot samovolně přecházet z tělesa chladnějšího na těleso teplejší
Nelze sestrojit periodicky pracující tepelný stroj, který by trvale konal práci pouze tím, že by ochlazoval jedno těleso, a k žádné další změně v okolí by nedocházelo

Třetí (Nernstův teorém)

Čistou pevnou látku nelze konečným pochodem ochladit na teplotu absolutní nuly (0 K; -273,15 °C), k této teplotě se lze pouze přiblížit
V roce 2017 byl třetí TD zákon odvozen a dokázán pomocí ostatních zákonů TD.

Vnitřní energie U

Stavová veličina – závisí na stavu systému, ale ne na tom, jak se systém do tohoto stavu dostal. Vnitřní energie je součet energie všech částic, které systém obsahuje. Lze ji také definovat jako součet kinetické a potenciální energie systému.

$$U = \sum_{i=0}^n \frac{1}{2}m_i v_i^2 + E_p$$

Její absolutní hodnotu nelze ani vypočítat, ani změřit, pouze její změny.

ΔU = ΔU₂ – ΔU₁

Ke změně vynitřní energie může dojít dvěma způsoby:

Konáním práce – stlačováním nebo expanzí plynu, třením těles, apod.
Tepelnou výměnou – ohřevem nebo ochlazením tělesa

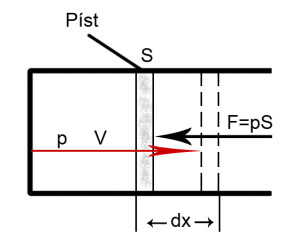
Objemová práce W

Práce, kterou systém vykonal nebo spotřeboval.

W = Fdx = pAdx = pdV

dV = SdX; S – plocha pístu

Pokud systém koná práci je W < 0; pokud ji přijímá je práce kladná.

Entalpie a entropie

Entalpie (H) vyjadřuje množství energie uložené v systému.

ΔH = ΔU + pΔV

Za izobarických podmínek je entalpie rovna množství tepelné energie (Q) v systému.

ΔH = Q

dH(S,p) = TdS + Vdp

Entropie (S) popisuje neuspořádanost systému, resp. počet stavů, které může systém nabýt. P_i označuje pravděpodobnost i-tého stavu.

$$S = -k\sum_i P_i \ln P_i$$

ΔS > 0 – spontánní proces
ΔS < 0 – proces probíhá v opačném směru
ΔS = 0 – rovnováha

Termochemie

Věda studující tepelné zabarvení reakcí.

Reakční teplo reakce a reakční teplo opačné reakce jsou až na znaménko stejná. Výsledná hodnota reakčního tepla nezávisí na průběhu chemické reakce, ale pouze na počátečním a konečném stavu.

ΔH > 0 – endotermní reakce
ΔH < 0 – exotermní reakce
ΔH = 0 – atermická reakce

Pro správný výpočet reakčního tepla je nutné znát skupenství všech látek v reakci.

CH₄(g) + 2 O₂(g) → CO₂(g) + 2 H₂O(g) ΔH = -802 kJ
CH₄(g) + 2 O₂(g) → CO₂(g) + 2 H₂O(l) ΔH = -890 kJ

Standardní spalné teplo – teplo, při kterém se spálí 1 mol látky v nadbytku kyslíku. Spalná tepla prvků jsou nenulová.

$$\Delta H_{298}^0 = \sum(\Delta H_{sp}^0)_{reakt} – \sum(\Delta H_{sp}^0)_{prod}$$ $$\Delta H_{298}^0 = \sum(\Delta H_{sl}^0)_{prod} – \sum(\Delta H_{sl}^0)_{reakt}$$

Standardní slučovací teplo – teplo, při kterém vzniká 1 mol látky přímo z prvků, reakční látky musí být ve standardní stavu. Standardní slučovací tepla prvků jsou rovna nule.

Látka	Skupenství	ΔH⁰_f[kJ.mol^-1]
I₂	s	0
I₂	g	+62
O₂	s	0
O₃	s	+142,7

Gibbsova energie G

Stavová funkce, jde o kritérium samovolnosti děje za izobaricko-izotermických podmínek.

ΔG⁰ – Gibbsova volná energie za standardních podmínek

298,15 K (25 °C)
100 000 Pa (1 bar) pro plyny
Koncentrace roztoků 1 M

Hodnoty ΔG⁰ jsou tabelovány.

$$\Delta G^0 = \Delta H^0 – T \Delta S^0$$

$$\Delta G^0_{reak} = \sum\nu_{prod}\Delta G^0_{sluc}(prod)\ – \sum\nu_{reakt}\Delta G^0_{sluc}(reakt)$$

ν – stechiometrický koeficient

Termodynamika ve formátu pdf.

Další kapitoly

One Reply to “Termodynamika”