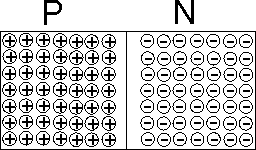
Na obrázku je krystal křemíku, jehož levá strana vykazuje vodivost typu P, a pravá strana vodivost typu N. V levé části krystalu jsou tedy obsaženy akceptory, které odevzdaly krystalové mříži kladně nabité díry, takže nyní jsou nabity záporně. Do pravé části byly naopak vpraveny donory, které dodaly do atomové mříže volné elektrony, a proto mají nyní kladný náboj.
Připojení přechodu PN na vnější napětí
Připojíme-li kladný pól baterie na oblast typu P a záporný pól na oblast typu N v krystalu křemíku nebo germania, začne krystalem procházet proud jehož velikost závisí na hodnotě vnějšího napětí.
Pokud je vnější napětí menší než je difuzní napětí přechodu (desetiny voltu), prochází přechodem jen velmi malý proud, protože oblast prostorového náboje má velký odpor (malou vodivost).
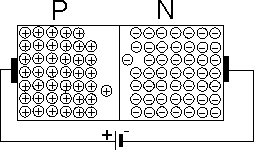
Pokud dosáhne vnější napětí hodnoty difúzního napětí (u germania asi 0,4 V, u křemíku asi 0,8 V) začně proud procházející přechodem prudce vzrůstat. To je způsobeno tím, že vnější napětí odpuzuje kladné díry z oblasti typu P do oblasti N a volné elektrony naopak, takže přechod PN je zaplaven nosiči náboje, čímž se jeho odpor prudce zmenšuje. Říkáme, že přechod PN je zapojen v propustném směru.
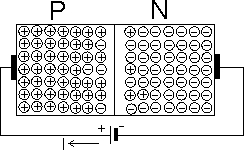
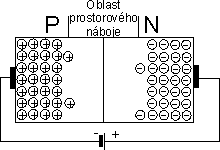
Pokud zaměníme polaritu vnějšího napětí, jsou díry i elektrony od přechodu odtahovány, čímž se rozšiřuje oblast prostorového náboje, který má nepatrnou elektrickou vodivost. Přechod je polarizován záporně a napětí působící na něm se označuje jako závěrné.
Matematický popis přechodu PN
Z fyzikální podstaty činnosti přechodu PN při vedení elektrického proudu vyplývá, že vztah mezi proudem a napětím na jeho svorkách je nelineární.
Samotný přechod PN lze popsat rovnicí
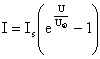 (1)
(1)
kde I je proud procházející přechodem při napětí U. Napětí U je kladné, je-li dioda pólována v propustném směru. Proud Is je tzv. nasycený (saturační) proud přechodu, který závísí na technologii a materiálu diody. Také značně závisí na teplotě, protože je tvořen tepelně generovanými dvojicemi elektron – díra. Teplotní závislost je exponenciální a proud Is2 při teplotě Q2 lze vypočítat z proudu Is1 při teplotě Q1 podle rovnice
![]() (2)
(2)
kde g je konstanta, jejíž velikost se pohybuje v rozmezí 0,06 – 0,1. Napětí UQ je tzv. teplotní potenciál
![]() (3)
(3)
kde k je Boltzmanova konstanta, q je elementární náboj, Q je absolutní teplota [K]. Korekční činitel m = 1 pro případ, že napětí na didoě je určeno pouze úbytkem vytvořeným difůzním proudem. Ve skutečné diodě se však uplatňuje i úbytek vytvořený tokem většinových nosičů, které kompenzují náboj menšinových nosičů a činitel m se pak mění v rozsahu 1 < m < 2. Pro napětí U >> UQ lze v rovnici (1) zanedbat jedničku proti exponenciále a dostaneme pro průběh voltampérové charakteristiky diody zapojené v prospustném směru přibližný vztah
![]() (4)
(4)
Pro závěrně pólovanou diodu platí
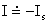
Literatura
- Shockley, W.; Bell System Technical Journal 1949, 28, 435-489. The theory of p-n junctions in semiconductors and p-n junction transistors. DOI: 10.1002/j.1538-7305.1949.tb03645.x
Další kapitoly
- Základy elektroniky
- Novinky
- Rezistory
- Kondenzátory
- Cívky
- Diody
- Diak
- Triak
- Tyristor
- Trisil
- Tranzistory
- Memristory
- Integrované obvody
- Výpočetní technika
- Komunikace
- Plošné spoje
- Baterie a akumulátory
- Čidla/sensory
- Datasheety