Chemické rovnice a stechiometrické výpočty – Web o chemii, elektronice a programování

Obsah

Chemická rovnice je symbolický zápis chemické reakce, reaktanty jsou obvykle na levé straně a produkty na pravé. Chemická rovnice musí být vyčíslena, tzn. u neredoxních procesů musí souhlasit počty atomů na levé a pravé straně, u redoxních dějů musí souhlasit i počet uvolněných a spotřebovaných elektronů, příp. náboje na obou stranách rovnice. Příkladem chemické rovnice je spalování vodíku v kyslíku:

2 H₂ + O₂ → 2 H₂O

Vyčíslování rovnice

Tady si můžete vyčíslování otestovat online.

Neredoxní rovnice

Neredoxní rovnice lze většinou vyčíslit intuitivně, např. reakce hydroxidu sodného s kyselinou sírovou:

NaOH + H₂SO₄ → Na₂SO₄ + H₂O

Vidíme, že v produktu jsou dva sodné ionty, proto k hydroxidu sodnému dáme dvojku a dopočítáme molekuly vody, výsledek pak je:

2 NaOH + H₂SO₄ → Na₂SO₄ + 2 H₂O

Složitější rovnice lze řešit pomocí soustavy matematických rovnic, např. pro rovnici:

a Ca₃P₂ + b H₂O → c Ca(OH)₂ + d PH₃

získáme následující soustavu rovnic pro jednotlivé prvky:

Ca: 3a = c
P: 2a = d
O: b = 2c
H: 2b = 2c + 3d

Dalším krokem je volba jednoho z koeficientů, v našem případě můžeme zvolit a=1, tím získáme c=3, b=6 a d=2. Jelikož jsou všechny koeficienty celočíselné, můžeme je doplnit do rovnice.

Ca₃P₂ + 6 H₂O → 3 Ca(OH)₂ + 2 PH₃

Tím máme rovnici vyčíslenou.

Redoxní rovnice

Redoxní rovnice jsou ty, kde se látky oxidují a redukují. Při oxidaci dochází k uvolňování elektronů a při redukci k jejich spotřebování, počet uvolněných elektronů musí odpovídat počtu elektronů, které se spotřebují na redukci. Příkladem může být rozpouštění mědi v kyselině dusičné.

Cu + HNO₃ → Cu(NO₃)₂ + NO + H₂O

Měď se oxiduje z Cu⁰ na Cu^II, tzn. že se uvolní dva elektrony. Redukuje se dusík z N^V na N^II, na což se spotřebují tři elektrony. Pro zjištění stechiometrických koeficientů použijeme křížové pravidlo.

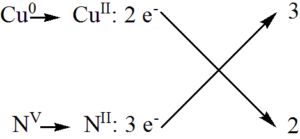
Z křížového pravidla vyplývá, že potřebujeme tři mědi a dva dusičnany, aby byla elektronová bilance v pořádku. Musíme také započítat správný počet molekul kyseliny dusičné, ze kterých vznikne dusičnan měďnatý. Vyčíslená rovnice tedy bude vypadat takto:

3 Cu + 8 HNO₃ → 3 Cu(NO₃)₂ + 2 NO + 4 H₂O

Šest elektronů uvolněných z mědi se spotřebuje na redukci dvou dusičnanů na oxid dusnatý.

Iontové rovnice

U těchto rovnic musíme kromě počtu atomů a vyměňovaných elektronů, hlídat i nábojovou bilanci. Tzn. že součet nábojů na levé straně musí odpovídat součtu nábojů na pravé straně rovnice:

2 Cu²⁺ + 4 I^– + H₂O → 2 CuI + I₂

Nábojová bilance: 2.2 + 4.(-1) = 4 – 4 = 0

Zvláštním typem redoxních reakcí jsou disproporcionace a komproporcionace.

Disproporcionace

Jedna sloučenina se zároveň oxiduje i redukuje, příkladem může být rozpouštění plynného chloru v hydroxidu sodném.

Cl₂ + 2 NaOH → NaCl + NaClO + H₂O

Nebo rozpouštění oxidu dusičitého ve vodě:

2 NO₂ + H₂O → HNO₃ + HNO₂

Komproporcionace

Dvě sloučeniny stejného prvku, v různých oxidačních stavech spolu navzájem reagují. Příkladem je oxidace manganaté soli roztokem manganistanu:

3 Mn²⁺ + 2 MnO₄^– + 2 H₂O → 5 MnO₂ + 4 H⁺

Nebo reakce probíhající v olověných bateriích:

Pb + PbO₂ + 2 H₂SO₄ → 2 PbSO₄ + 2 H₂O

Další informace v rovnicích

V rovnicích se často udává i skupenství reaktantů a produktů, k označení se používají zkratky uvedené v závorce za vzorcem.

Zkratka	Skupenství
s	pevné
l	kapalné
g	plynné
aq	vodný roztok

4 Fe(s) + 3 O₂(g) → 2 Fe₂O₃(s)

Nad a pod šipku se často zapisují informace o reakční teplotě, rozpouštědle, katalyzátoru, atd.

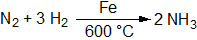
Stechiometrické výpočty

Stechiometrické výpočty, neboli výpočty z chemické rovnice umožňují snadno spočítat teoretický výtěžek reakce, příp. navážky reaktantů. Prvním krokem je napsání a vyčíslení správné rovnice. Např. pokud chceme spočítat kolik vody vznikne z 1,00 g plynného vodíku, napíšeme si rovnici:

2 H₂ + O₂ → 2 H₂O

z které vyplývá, že ze dvou molekul vodíku vzniknou dvě molekuly vody. Pro výpočet tedy budeme potřebovat látkové množství. Pro všechny členy chemické rovnice platí výraz:

$$\frac{n}{\nu} = konst$$

kde n je látkové množství a ν je stechiometrický koeficient dané látky. Pro naši rovnici tedy bude výraz vypadat takto:

$$\frac{n_{H_2}}{2} = \frac{n_{H_2O}}{2}$$

Vidíme tedy, že látkové množství vodíku a vody bude shodné. Látkové množství vypočítáme jako podíl hmotnosti a molární hmotnosti:

$$n_{H_2} = \frac{m_{H_2}}{M_{H_2}} = \frac{1,00}{2,02} = 0,50\ mol$$

Hmotnost vzniklé vody pak snadno spočítáme ze vztahu pro látkové množství.

$$m = n . M = 0,50 . 18,02 = 9,01\ g$$

Limitní reagent

Pokud do reakce nevstupují reaktanty v poměru, který odpovídá chemické rovnici, musíme nejprve určit, který reaktant bude určovat množství vzniklého produktu. Např. pokud potřebujeme spočítat množství produktu reakce (neutralizace) 5,00 g kyseliny šťavelové s 5,00 g hydroxidu sodného. Napíšeme si nejdříve rovnici:

(COOH)₂ + 2 NaOH → (COONa)₂ + 2 H₂O

Abychom zjistili, kterého reagentu bude nedostatek, tzn. který reagent bude určovat množství vzniklého šťavelanu sodného, musíme spočítat poměr $\frac{n}{\nu}$ pro všechny reaktanty. Výpočet je naznačen v tabulce:

	(COOH)₂	NaOH
m [g]	5,00	5,00
M [mol.g^-1]	90,03	40,00
$\frac{n}{\nu}$	0,056	0,063

Z tabulky vyplývá, že limitním reagentem bude kyselina šťavelová. Množství vzniklého šťavelanu sodného pak bude:

$$m = \frac{n.M}{\nu} = \frac{0,056 . 134,00}{1} = 7,50\ g$$

Pokud bychom k výpočtu použili navážku hydroxidu sodného, tak dostaneme výsledek:

$$m = \frac{n.M}{\nu} = \frac{0,125 . 134,00}{2} = 8,38\ g$$

Ale na přípravu 8,83 g šťavelanu sodného potřebujeme 5,63 g kyseliny šťavelové, do reakce jsme ovšem dali pouze 5,00 g. Proto vždy musíme hledat reaktant jehož poměr $\frac{n}{\nu}$ je pro danou reakci minimální.

Čistota výchozí látky

Nežijeme v ideálním světě, a často musíme využívat ne úplně čisté výchozí látky. To je nutné zohlednit ve výpočtu. Pokud budeme předpokládat, že nečistoty nám průběh reakce neovlivní, je situace poměrně jednoduchá.

Kolik zelené skalice vznikne reakcí 10 g železných pilin s nadbytkem zředěné kyseliny sírové? Železo má čistotu 85 %.

Zelená skalice je heptahydrát síranu železnatého, reakce bude probíhat takto:

Fe + H₂SO₄ + 7 H₂O → FeSO₄.7H₂O + H₂

Prvním krokem bude výpočet hmotnosti čistého železa, k tomu stačí obyčejná trojčlenka nebo využijeme hmotnostní zlomek:

m(Fe) = m . 0,85 = 10 g . 0,85 = 8,5 g

Pak už je výpočet snadný:

Látka	M [g.mol^-1]	m [g]	n [mol]
Fe	55,84	8,5	0,15
FeSO₄.7H₂O	278,01	42,31	0,15

Reakcí tedy vznikne 42,31 g zelené skalice.

Výtěžek reakce

Většina reakcí neprobíhá ze sta procent, ale získáme pouze část očekávaného produktu. To je také nutné zohlednit při výpočtu.

Kolik jodidu olovnatého vznikne reakcí 10,0 g Pb(NO₃)₂ s KI, průměrný výtěžek reakce je 88 %.

Pb(NO₃)₂ + 2 KI → PbI₂ + 2 KNO₃

Z jednoho molu dusičnanu olovnatého nám vznikne jeden mol jodidu:

Látka	M [g.mol^-1]	m [g]	n [mol]
Pb(NO₃)₂	331,21	10,0	0,03
PbI₂	461,01	13,92	0,03

Pokud by byl výtěžek reakce 100 %, získali bychom 13,92 g. Jelikož je ale jen 88 % bude reálný zisk jodidu nižší:

m = 13,92 . 0,88 = 12,25 g PbI₂

Reakcí získáme 12,25 g jodidu olovnatého.

Reakce s plyny

Pokud se v reakci vyskytují plynné látky, budeme zpravidla potřebovat pro výpočet látkového množství molární objem:

$$n = \frac{V}{V_m}$$

hodnota molárního objemu je za standardních podmínek 22,414 dm³.mol^-1, tato hodnota je platná pro ideální plyny, u reálných se bude lišit.

Příklad: Kolik litrů CO₂ (měřeno za standardních podmínek) se uvolní termickým rozkladem 1 kg vápence o čistotě 90 %?

Nejprve si napíšeme a vyčíslíme reakci, v tomto případě je to jednoduché, uhličitan vápenatý (vápenec) se rozkládá na oxid vápenatý (pálené vápno) a oxid uhličitý:

CaCO₃ → CaO + CO₂

Vápenec obsahuje 10 % nečistot, tzn. že do reakce vstoupí pouze 0,9 kg CaCO₃.

$$n = \frac{m}{M} = \frac{900}{100,09} = 9,0\ mol\ CaCO_3$$

Z 9 molů vápence vznikne 9 molů oxidu uhličitého, jeho objem spočítáme snadno:

$$V = n.V_m = 9,0 . 22,414 = 201,7\ dm^3\ CO_2$$

Řešené příklady

Pokud si chcete procvičit stechiometrické výpočty, můžete zkusit vypočítat těchto pár příkladů, na stránce je uvedeno i řešení.