Lineární regrese – Web o chemii, elektronice a programování

Lineární regrese je důležitá metoda, jak z experimentálně naměřených bodů získat přímku. V dnešní době se to samozřejmě dělá s pomocí vhodného softwaru, ale v tomto článku si ukážeme, jak získat rovnici regresní přímky výpočtem.

Z měření získáme takovou tabulku dat:

x	y
1	0,4
2	1,85
3	3,3
4	4,2
5	5,5
6	5,9
7	6,99
8	8,8
9	9,2
10	10,6

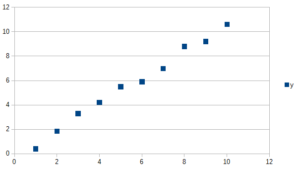
Je vidět, že body na přímce neleží. Existuje několik metod, jak spočítat rovnici regerese. Nejjednodušší pro ruční výpočet je metoda nejmenších čtverců. Rovnice přímky má obecný tvar:

$$y = ax + b$$

a je směrnice přímky a b je úsek na ose y. Koeficienty vypočítáme pomocí vzorců:

$$a = \frac{\sum x \sum y – n\sum (xy)}{(\sum x)^2 – n\sum x^2}$$

$$b = \frac{\sum x \sum (xy) – \sum (x^2)\sum y}{(\sum x)^2 – n\sum x^2}$$

kde n je počet bodů.

Tabulku bude nutné pro výpočet rozšířit:

#	x	y	x²	xy
1	1	0,4	1	0,4
2	2	1,85	4	3,7
3	3	3,3	9	9,9
4	4	4,2	16	16,8
5	5	5,5	25	27,5
6	6	5,9	36	35,4
7	7	6,99	49	48,93
8	8	8,8	64	70,4
9	9	9,2	81	82,8
10	10	10,6	100	106
∑	55	56,74	385	401,83

Získané součty dosadíme do rovnic:

$$a = \frac{\sum x \sum y – n\sum (xy)}{(\sum x)^2 – n\sum x^2} = \frac{55 * 56,74 – 10 * 401,83}{55^2 – 10 * 385} = 1,088$$

$$b = \frac{\sum x \sum (xy) – \sum (x^2)\sum y}{(\sum x)^2 – n\sum x^2} = \frac{55 * 401,83 – 385 * 56,74}{55^2 – 10 * 385} = -0,31$$

Rovnice regrese je tedy:

$$y = 1,09x – 0,31$$

Grafické zobrazení:

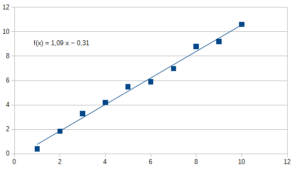
Toto je jednoduchá ukázka, jak spočítat lineární regresi pro sadu dat. Samozřejmě jednodušší je využít tabulkový procesor, nebo kalkulačku se statistickými funkcemi.

Další kapitoly