S tvorbou kalibrační křivky se setkal skoro každý, kdo se dostal do laboratoře, ať už během výuky nebo zaměstnání. V tomto článku bych chtěl ukázat, jak tento úkol zvládnout s využitím LibreOffice Calc a GNUPlotu. Ukázka ručního výpočtu je zde.
Kalibrační křivka
Kalibrační křivka slouží pro stanovení závislosti měřené veličiny na (nejčastěji) koncentraci, ale může jít i o teplotu, vlhkost, atd. My využijeme data ze spektrofotometrie, půjde tedy o závislost absorbance (A) na koncentraci (c).
$$\textrm{A} = f(\textrm{c})$$
| Koncentrace [mol.dm-3] | Absorbance |
|---|---|
| 0,0 | 1,339 |
| 0,05 | 1,347 |
| 0,1 | 1,377 |
| 0,2 | 1,379 |
| 0,4 | 1,408 |
| 0,6 | 1,455 |
| 0,8 | 1,579 |
| 1,0 | 1,584 |
| 1,2 | 1,967 |
Body lze proložit několika metodami, pokud je závislost lineární, používá se nejčastěji metoda nejmenších čtverců.[1]
LibreOffice Calc
LibreOffice je balíček kancelářských aplikací, my využijeme aplikaci Calc.[2] Před delší dobou jsem zde zveřejnil návod na psaní matematických vzorců v tomto programu.
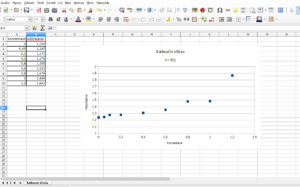
Prvním krokem je vložení dat do tabulky a z této tabulky vytvoříme graf (XY (bodový) → Pouze body).
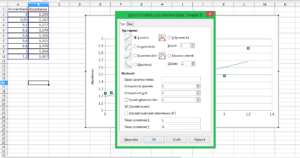
V grafu klikneme pravým tlačítkem na jeden z bodů a z menu zvolíme položku „Vložit spojnici trendu“. Zde zvolíme lineární regresi, zaškrtneme „Zobrazit rovnici“ a ve spodní části dialogu můžeme pojmenovat proměnné.
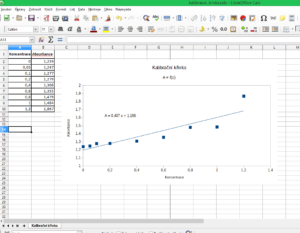
Získaná křivka bude vypadat nějak takto:
Rovnici regrese můžeme využít pro výpočet koncentrace neznámého roztoku, u kterého jsme změřili absorbanci, např. pro absorbanci 1,285 získáme koncentraci jednoduchou úpravou rovnice:
$$\textrm{c}\ =\ \frac{\textrm{A}-1,196}{0,407}\ =\ \frac{1,285-1,196}{0,407}=0,22\ \textrm{mol.dm}^{-3}$$
Pokud chceme spočítat směrnici nebo úsek na ose y použijeme funkce SLOPE resp. INTERCEPT, pro náš příklad by byl správný tvar:
Směrnice: =SLOPE(B2:B10;A2:A10)
Úsek na ose y: =INTERCEPT(B2:B10;A2:A10)
Vzorový soubor pro LibreOffice Calc si můžete stáhnout zde.
Gnuplot
O Gnuplotu[3] jsem tady už pár článků zveřejnil, takže bez větších úvodů přejdeme k akci.
Data si připravíme do obyčejného textového souboru, který nazveme kalibracni_krivka.data, hodnoty x a y jsou odděleny mezerami. Měl by vypadat nějak takto:
0.0 1.339 0.05 1.347 0.1 1.377 0.2 1.379 0.4 1.408 0.6 1.455 0.8 1.579 1.0 1.584 1.2 1.967
Pro vykreslení bodů do PNG souboru použijeme tento jednoduchý kód:
set xrange [0 : 1.4] set yrange [1.2 : 2.2] set terminal png set output 'kalibracni_krivka.png' plot 'kalibracni_krivka.data' using 1:2 title '' with points
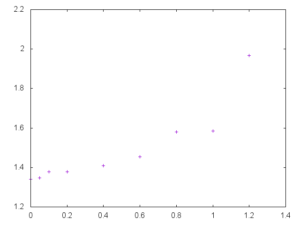
Získáme takový výstup:
Regresní křivku získáme přidáním tří řádků:
set xrange [0 : 1.4]
set yrange [1.2 : 2.2]
set terminal png
set output 'kalibracni_krivka.png'
f(x)=m*x + b
fit f(x) 'kalibracni_krivka.data' using 1:2 via m,b
plot 'kalibracni_krivka.data' using 1:2 title '' with points,\
f(x) title 'Lineární regrese'
První z přidaných řádků:
f(x)=m*x + b
definuje funkci, kterou chceme použít pro regresi, v našem případě jde o přímku. Další řádek
fit f(x) 'kalibracni_krivka.data' using 1:2 via m,b
provede optimalizaci parametrů m a b, tj. směrnice přímky a úseku na ose y, tak aby byla regrese co nejvýhodnější.
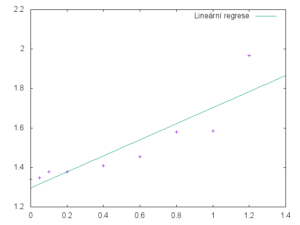
Výstup pak bude vypadat takto:
Parametry lineární regrese najdeme v souboru fit.log.
*******************************************************************************
Tue Apr 25 19:41:41 2017
FIT: data read from 'kalibracni_krivka.data' using 1:2
format = x:z
x range restricted to [0.00000 : 1.40000]
#datapoints = 9
residuals are weighted equally (unit weight)
function used for fitting: f(x)
f(x)=m*x + b
fitted parameters initialized with current variable values
iter chisq delta/lim lambda m b
0 6.0917500000e-01 0.00e+00 8.38e-01 1.000000e+00 1.000000e+00
4 6.3573208602e-02 -1.23e-08 8.38e-05 4.071398e-01 1.295994e+00
After 4 iterations the fit converged.
final sum of squares of residuals : 0.0635732
rel. change during last iteration : -1.23119e-013
degrees of freedom (FIT_NDF) : 7
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 0.0952989
variance of residuals (reduced chisquare) = WSSR/ndf : 0.00908189
Final set of parameters Asymptotic Standard Error
======================= ==========================
m = 0.40714 +/- 0.07655 (18.8%)
b = 1.29599 +/- 0.04876 (3.763%)
correlation matrix of the fit parameters:
m b
m 1.000
b -0.759 1.000
V oddíle „Final set of parameters“ najdeme parametry rovnice regrese, v našem případě je rovnice:
$$\textrm{A}\ =\ 0.407 \textrm{c} + 1.296$$
Ta je mírně odlišná od rovnice získané z LibreOffice, to je dáno jiným přístupem k výpočtu.
Archív se všemi soubory můžete stáhnout zde.
Literatura
- Metoda nejmenších čtverců
- LibreOffice.org
- gnuplot
- Lineární regrese na tomto webu