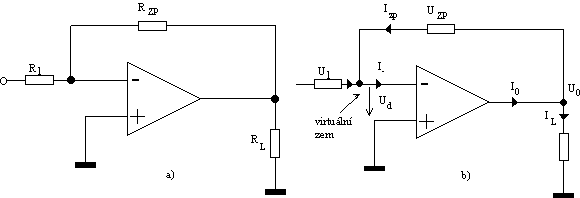
a) Zapojení invertujícího zesilovače. R1 je vstupní odpor, Rzp je zpětnovazební odpor a RL je výstupní odpor.
b) Rozložení napětí a proudů u invertujícího zesilovače.
Invertující zesilovač patří mezi nejčastější zapojení OZ. Pracuje tak, že signál přichází do invertujícího vstupu (-), zatímco druhý neinvertující vstup (+) je uzeměn. K výstupu je připojena jednak zátěž RL proti zemi a dále zpětnovazebný odpor RZP. Vstupní signál prochází odporem R1, který svou velikostí zároveň určuje vstupní odpor, kterým se invertující zesilovač projevuje.
Připojíme-li na vstup napětí U1 rozloží se celé na odporu R1. A protože na invertujícím vstupu je uzel s nulovým napětím, tzv. virtuální zem, začne obvodem téci proud I1. Do invertujícího vstupu teče proud také zpětnovazebním odporem RZP. Podle Ohmova zákona mají tyto proudy velikost
U zpětnovazebného odporu je záporné znaménko, protože podle Kirchhoffova zákona je součet vstupního a výstupního proudu roven 0 (I1 + (- IZP) = 0). Toto potvrzuje, že invertující vstup má nulový potenciál, ačkoliv není uzeměn. Neinvertující vstup je uzeměn přímo, takže jsou oba dva vstupy na nulovém potenciálu. Vztahy vyjadřující činnost OZ platí za předpokladu, že OZ pracuje s nekonečně velkým zesílením a nulovými vstupními proudy. V tomto případě je vstupní proud do invertujícího vstupu označen I–. Dále se předpokládá, že zesilovač má nulové diferenční napětí Ud mezi oběma vstupy. Z výstupu teče proud I0 jednak do zpětné vazby IZP a také IL zatěžovacím odporem RL k zemi. Platí, že I0 = IZP + IL.
Z těchto vztahů lze vyjádřit rovnici, která platí pro ideální zesilovač
Výstupní napětí U0 je přímo úměrné výstupnímu napětí U1 a zpětnovazebnímu odporu RZP. Nepřímo úměrné je vstupnímu odporu R1. Čím větší bude zpětnovazební odpor a čím menší vstupní odpor, tím bude větší zesílení na výstupu. Záporné znaménko na pravé straně znamená, že zvětšující se kladné napětí na invertujícím vstupu vyvolá zvětšující se záporné napětí na výstupu. Přivedeme-li na vstup střídavý signál, pak signál na výstupu je posunut o 180°. Tato inverzní funkce dala jméno zesilovači.
Literatura
Václav Malina; Poznáváme elektroniku III, nakladatelství Kopp, České Budějovice, 1997