Tyto metody jsou charakterizovány změnou entropie při přechodu atomu nebo molekuly dané látky z fáze 1 do fáze 2. Pokud bude entropie S2 fáze 2 menší než S1fáze 1 a přechod bude izotermický (T = konst.), tak bude vyžadovat dodání latentního tepla L z okolí:
L = T(S1 – S2) (1)
Toto teplo může dodat vzorek, který chceme ochladit.
Odpařování kapalin
Tato technika byla použita při prvním zkapalnění helia a je dodnes využívána ve většině ledniček. Její princip spočívá v tom, že při odpařování ztrácí kapalina atomy s nejvyšší energií a tím se ochlazuje. Tyto atomy získávají potřebnou energii od svých sousedů – to je ta latentní energie (viz vztah výše). Zvýšení výkonu tohoto typu chladících zařízení je možné dosáhnout pouze dosažením vyššího výkonu odpařování.
Atom, který má uniknout z kapaliny do páry musí získat dostatečnou energii od svých sousedů, ale to je se snižující se teplotou stále více obtížné, protože průměrná energie částic klesá. Proto je potřeba stále vyšší množství srážek, z toho důvodu počet atomů nv, který opustí objem kapaliny klesá s teplotou exponenciálně.
$$n_v \approx e^{\frac{U}{k_BT}} \quad \textrm{(2)}$$
kde U = L = Q = T(S1 – S2) je energetická bariéra, kterou musí částice překonat.
Tlak par, úměrný počtu částic nad kapalinou, klesá v důsledku vztahu (2) exponencielně. Např. při teplotě 1 K je tlak nasycené rovnovážné páry na kapalným 4He asi 13,3 Pa a při teplotě 0,15 K již jen 133,6 . 10-18 Pa (tato hodnota zhruba odpovídá vakuu v mezihvězdném prostoru). A pro dosažení teploty 0,03 K odpařováním kapaliny by bylo potřeba snížit tlak páry nad kapalinou na nereálnou hodnotu 133,3 . 10-100 Pa.
Metoda odčerpávání par je vhodná pro ochlazení izotopu 4He na teplotu 0,8 – 4,2 K a izotopu 3He na teplotu 0,3 – 3,3 K.
Rozpouštění 3He v 4He
Tato metoda je založena na nestabilitě roztoku 3He a 4He a umožňuje dosáhnout teplot 300 mK – 1,9 mK. Oba izotopy mají stejné elektronové obálky (2 elektrony v orbitalu 1s), ale liší se jaderným spinem. Izotop 4He má spin I = 0 a hodnota spinu 3He je I = ½. Dalším důležitým rozdílem je to, že ve výše uvedeném teplotním intervalu je 4He již supratekuté (má viskozitu rovnu nule). Nesupratekuté atomy 3He se v takovém prostředí pohybují jako kvaziplyn a supratekutá složka se chová v podstatě jako vakuum (neinteraguje s nimi). V tomto „vakuu“ mohou atomy 3He obsadit jen takový objem, jaký jim umožní atomy 4He. Přítomnost 4He změní jak setrvačné vlastnosti 3He tak i jeho hmotnost.
Až do teploty 0,87 K je možné obě kapaliny míchat v libovolném poměru, ale pod touto teplotou se homogenní roztok začne rozpadat na silně a slabě koncentrovanou směs. Důvodem této separace je rozdíl v nulové energii E0 = Δp2/2m atomů 3He a 4He. Protože je atom 3He lehčí něž atom 4He je jeho energie E0 větší, takže se kapalné 3He začne oddělovat od „pomalejšího“ 4He. Při teplotě menší než 0,1 K má bohatší fáze koncentraci 3He již 99,99 %. Ale i při teplotě absolutní nuly zůstává rovnovážná koncentrace 3He ve zředěné fázi kolem 6,4 %.
V tomto procesu je také důležité to, že atom 3He je fermion (má spin ½ a tedy individualistická částice, ale atom 4He (I = 1) je boson, čili částice s „kolektivními sklony“. Bosony mohou všechny obsadit jeden kvantový stav, zatímco fermiony budou obsazovat stále vyšší a vyšší energetické stavy v prostoru hybností a vytvoří tzv. Fermiho kapalinu. Při teplotě nižší než 0,87 K začne docházet k spontánnímu oddělování těchto dvou kapalin.
Pokud budeme z fázově rozděleného systému odčerpávat atomy 3He přes „supratekuté vakuum“ 4He dojde díky výparnámu teplu tohoto fázového přechodu k ochlazení směsi. Na rozdíl od obyčejného odpařování má tento proces výparné teplo silně závislé na teplotě:
L = T ΔS = 84 T2
Dalším rozdílem oproti obyčejnému odpařování je to, že tento proces není spojen s exponenciálním poklesem počtu odpařovaných atomů. Jejich počet je téměř nezávislý na teplotě.
Díky těmto závislostem neklesá chladící výkon \(\dot{Q} = L\dot{n}\) exponenciálně, ale jako T-2:
$$\dot{Q} = L\dot{n} = 84T^2$$
tečka nad symbolem označuje derivaci podle času a \(\dot{n}\) počet molů odpařených z povrchu, který rozděluje dvě fáze, za jednotku času.
Odčerpáváním 3He ze spodní zředěné fáze se porušuje rovnovážný stav u rozhraní a dochází ke vzniku osmotického tlaku. Ten umožňuje trvalý přechod atomů 3He přes fázové rozhraní do chudší směsi. Zvýšení účinnosti tohoto procesu dosáhneme cirkulací 3He a příp. i 4He.
Nejnižší dosažitelná teplota tímto procesem je 1 mK. Nižší teplotu nelze dosáhnout z několika důvodů:
- nedokonalost tepelných výměníků, jejich malá účinnost, malá plocha, viskózní ohřev (viskozita roste s klesající teplotou jako T-2),
- zpětný tepelný tok sloupcem zředěné fáze,
- přímý tepelný tok přitékajícího koncentrovaného 3He,
- viskózní ohřev, způsobený velkou viskozitou kapaliny odcházející ze směšovací komory,
- přítok tepla způsobený vibracemi aparatury,
- ohřátí Foucaultovými vířivými proudy z vnějších elektromagnetických zářičů
Tato metoda již má poměrně dlouhou historii. V roce 1956 objevili fyzikové G. K. Walters a W. M. Fairbank fázovou separaci izotopů helia. První rozpouštěcí refrigátor sestrojili v roce 1964 v Holandsku P. Das, R. de Bruyn Ouboter a K. W. Taconis, ale podařilo se jim dosáhnout jen teploty 0,22 K. Krátce poté, v roce 1966 dosáhli H. E. Hall, P. J. Ford a K. Thomson teploty 0,55 mK. Rekordní teploty 1,9 mK dosáhli v Leydenské laboratoři v Holandsku roku 1987 Vermeulen a Frossati.
Dnes patří tato metoda mezi nejpoužívanější pro teploty v oblasti mK.
Změna entropie při přechodu z kapaliny do pevné fáze
Tuto metodu předpověděl v roce 1950 sovětský fyzik Isaak Yakovlevich Pomerančuk. Je založena na skutečnosti, že při teplotách pod 300 mK je entropie Sl kapalného 3He překvapivě nižší než entropie Ss pevného 3He. Pevné 3He získáme stlačením kapaliny na 2,8 MPa. Kapalné 3He se chová jako normální Fermiho kapalina a jeho entropie Sl klesá lineárně s teplotou. Pevné 3He má však entropii při vyšších teplotách „zamrzlou“ na hodnotě Ss = R ln2, kde R je molární plynová konstanta a ln2 plyne z hodnoty ln(2I + 1) pro spin 3He (I = ½). Tato hodnota entropie odpovídá totální dezorientaci jaderných spinů v 3He. Při těchto teplotách je totiž tepelná energie kBT stále ještě veliká ve srovnání s malými mezijadernými interakcemi (slabé překrytí vlnových funkcí atomů 3He – tzv. výměnná jaderná interakce) a 3He se chová jaké téměř ideální paramagnetická látka. V krystalové mříži 3He jsou atomy téměř lokalizovány do svých mřížkových poloh. Přesto je jejich rozkmit kolem rovnovážných poloh veliký (až 30 % meziatomové vzdálenosti), což umožňuje výměnné interakce, které jsou až o tři řády silnější než dipolární magnetické interakce. Tyto výměnné interakce přivedou nakonec při klesající teplotě soustavu spinů do kooperativního stavu. Proto entropie při teplotách blížících se tomuto fázovému přechodu v oblasti 1 mK začne rychle klesat.
V kapalině jsou však atomy v rychlém pohybu a jejich statistika se neřídí Boltzmannovou statistikou, která platí pro paramagnetika s lokalizovanými spiny. V kapalině musíme použít Fermiho-Diracovu statistiku, která je vhodná pro delokalizované nebo volné atomy 3He. V prostoru hybností dochází k uspořádání spinů jader podle Pauliho vylučovacího principu: na každé energetické hladině mohou být pouze dva fermiony s opačnými spiny. Tyto fermiony jsou seřazeny v prostoru hybností podle energií v tzv. Fermiho kouli, jejíž poloměr odpovídá maximální hybnosti jader 3He. Paramagnetismus takové soustavy je teď soustředěn do malé oblasti (kBT) kolem povrchu Fermiho koule. Z teorie kovů a z teorie Fermiho kapalin vyplývá, že tento tzv. Pauliho paramagnetismus je mnohem slabší než paramagnetismus lokalizovaných magnetických dipólů v pevném 3He. V kapalině se tohoto paramagnetismu účastní pouze malá část nespárovaných spinů kolem povrchu Fermiho koule, zatímco v pevném heliu se paramagnetismu účastní všechny lokalizované atomy. Proto je entropie Sl < Ss. Fyzikálně tento rozdíl spočívá v rozdílu statistik popisujících kapalné (delokalizované fermiony) a pevné 3He (lokalizované fermiony).
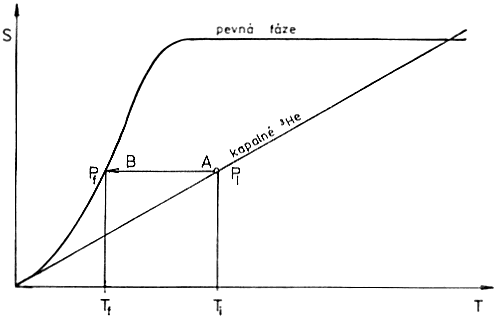
Na obr. 1 vidíme, že vyjdeme-li z bodu z bodu A při počáteční teplotě Ti a provedeme-li adiabatickou krystalizaci při konstantní entropii, pak se dostaneme do bodu B s konečnou teplotou Tf < Ti.
Chladící výkon ![]() bude nyní podle rovnice (1) roven
bude nyní podle rovnice (1) roven
$$\dot{Q} = (S_s – S_l)T\dot{n}$$
kde \(\dot{n}\) je časová změna převodu atomů z jednoho molu kapalin do pevné fáze za sekundu. Takže chladící výkon je lineárně závislý na teplotě. To je velmi důležitý fakt pro využití této chladící metody, bohužel jsou v tomto případě velké technické obtíže s realizací (nesmí docházet k přeměně mechanické energie na teplo, díky výměnným interakcím je omezena nejnižší dosažitelná teplota, atd.), díky kterým se tato metoda používá pouze v některých speciálních případech. První, kdo tuto metodu realizoval, byl sovětský fyzik J. D. Anufrijev, který v roce 1965 ochladil 3He z teploty 50 mK na 18 mK. Američtí fyzikové D. D. Osheroff, R. G. Richardson a D. M. Lee pak dovedli tuto metodu až do oblasti jednoho mK.