pH, aktivita roztoku – Web o chemii, elektronice a programování

Obsah

V tomto článku budeme potřebovat logaritmy, své znalosti tohoto tématu si můžete osvěžit např. na serveru matematika.cz. Také doporučuji pěknou přednášku na youtube.

Aktivita roztoku

Aktivita (a) popisuje reálné chování roztoku. Aktivita jakékoliv čisté látky v jejím standardním je definitoricky jednotková.

μ_i = μ_i⁰ + RT ln a_i

μ_i – chemický potenciál, μ_i⁰ – standardní chemický potenciál

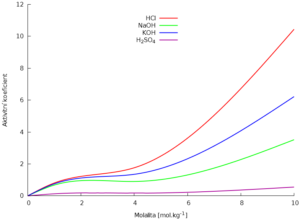
Aktivitu lze vyjádřit jako součin molární koncentrace a aktivitního koeficientu.

a = γc

Aktivitní koeficient popisuje rozdíl mezi ideálním chováním vyjádřeným koncentrací a reálným chováním, které popisuje aktivita. Je úměrný náboji iontů v roztoku a iontové síle roztoku.

log γ = -0,509z²·√I

I – iontová síla roztoku, popisuje množství iontů v roztoku.

$$I = \frac{1}{2}\sum^n_{i=0} c_iz_i^2$$

c_i – molalita, z_i – náboj, 0,509 – konstanta pro vodné roztoky.

Střední aktivitní koeficienty ve vodných roztocích při 25 °C

c_m[mol.kg^-1]	0,1	1,0	4,0	10,0
HCl	0,796	0,809	1,762	10,44
NaOH	0,766	0,678	0,903	3,52
KOH	0,798	0,756	1,352	6,22
H₂SO₄	0,265	0,130	0,171	0,553
AgNO₃	0,734	0,429	0,210	–
Ca(NO₃)₂	0,48	0,35	0,42	–

Závislost aktivitních koeficientů na koncentraci

Zdroj dat: Vohlídal, Jiří. Chemické tabulky. Praha: SNTL, 1982.

pH

pH (Potential of Hydrogen) je číslo, které vyjadřuje, zda daný roztok reaguje kysele, neutrálně nebo zásaditě. Ve vodných roztocích se hodnoty pH pohybují v intervalu od 0 do 14. Pokud má roztok hodnotu pH 7 je neutrální, nižší hodnoty odpovídají kyselému prostředí, vyšší zásaditému.

Hodnota pH je dána koncentrací H⁺ iontů v roztoku, jde o logaritmickou stupnici, změna koncentrace o jeden řád se projeví změnou hodnoty pH o jedničku.

Kyseliny a zásady

Podrobněji zde.

Arrheniova teorie definuje kyseliny jako látky, které ve vodném roztoku uvolňují ionty H⁺ (H₃O⁺), zásady pak uvolňují OH^–.

Brønstedova teorie definuje kyseliny jako donory protonů a zásady jako jejich akceptory.

Lewisova teorie definuje kyseliny jako akceptory elektronových páru a zásady jako jejich donory.

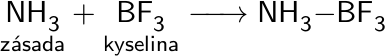
Silné kyseliny a zásady ve vodném roztoku zcela disociují.

HCl + H₂O → H₃O⁺ + Cl^–

NaOH → Na⁺ + OH^–

Slabé kyseliny a zásady disociují pouze z části. Síla kyseliny a zásady je dána disociační konstantou pK_a nebo pK_b.

$$K_a = \frac{[H_3O^+][Cl^-]}{[HCl]}$$

$$K_b = \frac{[OH^-][NH_3^+]}{[NH_3]}$$

pK_a = -log K_a; pK_b = -log K_b

Kyselina	pK_a
H₃PO₄	pK_a1 2,16 pK_a2 7,21 pK_a3 12,32
Fenol	10
HClO	7,53
HF	3,2
HCl	-7

Konjugované páry kyselina-zásada

Konjugované páry jsou dvojice částic vznikající disociací, liší se o H⁺.

HCl + H₂O → H₃O⁺ + Cl^–

Konjugovaná zásada k silné kyselině je slabá zásada.

HCl → Cl^–

Konjugovaná kyselina k slabé zásadě je silná kyselina.

H₂O → H₃O⁺

Autoionizace vody

Voda je amfoterní, tzn. že se chová jako kyselina i jako zásada.

2 H₂O → H₃O⁺ + OH^–

Iontový součin vody je součin rovnovážné koncentrace iontů. Jeho hodnota je pro dané rozpouštědlo a teplotu konstantní.

K_W = [H⁺][OH^–] = 1.10^-14 mol.dm^-3

pK_W = -log K_W = 14

Pro konjugovaný pár kyselina-zásada platí:

K_aK_b = K_W

pK_a + pK_b = pK_W

pH a pOH

pH = -log a_H3O+ = -log[H₃O⁺]

pOH = -log a_OH- = -log[OH^–]

pH + pOH = 14,00

Pokud je ph<7, roztok je kyselý, pokud je pH>7, roztok je zásaditý. Neutrální roztok má pH=7.

pH	pOH	[H⁺]	[OH^–]
2	12	0,01	10^-12
4	10	0,0001	10^-10
6	8	10^-6	10^-8
7	7	10^-7	10^-7
8	6	10^-8	10^-6
10	4	10^-10	0,0001
12	2	10^-12	0,01
14	0	10^-14	1,0

Výpočet pH

Silné kyseliny a zásady

Silné kyseliny a zásady jsou v roztoku zcela disociovány. Pro silnou kyselinu platí vztah:

pH = -log[H⁺]

Pokud se jedná o silnou jednosytnou kyselinu, např. HCl, můžeme vztah zjednodušit:

pH = -log c_kys

U silných zásad vycházíme ze vztahu mezi pH a pOH ve vodných roztocích:

pH = 14 – pOH

Pro silnou jednosytnou zásadu, např. NaOH, pak získáme vztah:

pH = -log[H⁺] = 14 + log c_zas

Slabé kyseliny a zásady

Slabé kyseliny a zásady jsou v roztoku disociovány pouze částečně. Míru disociace popisuje rovnovážná konstanta:

HA ⇌ H⁺ + A^–

$$\textrm{K = }\frac{[\textrm{H}^+][\textrm{A}^-]}{[\textrm{HA}]}$$

Z rovnice disociace vyplývá, že koncentrace H⁺ a A^– iontů budu stejné. Rovnovážná koncentrace nedisociované kyseliny bude rovna rozdílu výchozí koncentrace a rovnovážné koncentrace H⁺ iontů. Proto můžeme vztah upravit následovně:

$$\textrm{K = }\frac{[\textrm{H}^+][\textrm{H}^+]}{\textrm{c}_0\ -\ [\textrm{H}^+]} \\
\textrm{K = }\frac{[\textrm{H}^+]^2}{\textrm{c}_0\ -\ [\textrm{H}^+]}$$

Pro slabé kyseliny můžeme zavést i předpoklad, že výchozí koncentrace kyseliny je řádově vyšší než koncentrace iontů, tím získáme zjednodušený vztah, z kterého snadno vyjádříme koncentraci H⁺:

$$\textrm{K}_\textrm{a}\ =\ \frac{[\textrm{H}^+]^2}{\textrm{c}_0} \\
[\textrm{H}^+] = \sqrt{\textrm{K}_\textrm{a}\ .\ \textrm{c}_0}$$

Logaritmováním tohoto vztahu získáme finální podobu:

$$\textrm{pH = }\frac{1}{2}\textrm{pK}_\textrm{a} – \frac{1}{2}\log \textrm{c}_0$$

Pro zásady musíme využít příslušnou disociační konstantu pK_b, vztah pro pH má podobu:

$$\textrm{pH = 14 – }\frac{1}{2}\textrm{pK}_\textrm{b} + \frac{1}{2}\log \textrm{c}_0$$

Hodnoty disociačních konstant můžeme najít v chemických tabulkách, hodnoty pro vybrané kyseliny a zásady jsou uvedeny zde.

Soli silné kyseliny i zásady

NaCl + H₂O → Na⁺ + Cl^– + H₂O

KNO₃ + H₂O → K⁺ + NO₃^– + H₂O

Při disociaci nedochází k ovlivnění koncentrace protonů ani OH^–, proto nebude pH roztoku těmito solemi ovlivněno.

Soli slabých kyselin a zásad

Při disociaci solí slabých kyselin dochází ke vzniku iontů H⁺ nebo OH^– a tím i k ovlivnění hodnoty pH.

Sůl slabé zásady a silné kyseliny způsobuje nárůst koncentrace H⁺ iontů a tím dochází ke snížení hodnoty pH:

NH₄NO₃ + H₂O → NH₄⁺ + NO₃^– + NH₃ + H⁺

pH = 7 – 1/2(pK_b + log c)

Sůl slabé kyseliny a silné zásady způsobuje nárůst koncentrace OH^– iontů a tím dochází ke zvýšení hodnoty pH:

NaF + H₂O → Na⁺ + F^– + HF + OH^–

pH = 7 + 1/2(pK_a + log c)

Při disociaci soli slabé kyseliny i zásady dochází ke vzniku iontů H⁺ i OH^–. Poměr disociačních konstant pak určuje, jestli hodnota pH naroste nebo klesne.

NH₄F + H₂O → NH₄⁺ + F^– + NH₃ + H⁺ + HF + OH^–

pH = 7 + 1/2(pK_a – pK_b)

pK_a(HF) = 3,17

pK_b(NH₃) = 4,75

pH = 7 + 1/2(3,17 – 4,75) = 6,21

pH roztoku soli slabé kyseliny a zásady nezávisí na koncentraci, ale pouze na jejich disociačních konstantách.

Pufry, tlumivé (ústojné) roztoky

Jde o roztoky, které se používají pro stabilizaci pH během reakce, příp. měření. Jsou složeny ze slabé kyseliny a její soli, příp. ze slabé zásady a její soli. Příkladem může být acetátový pufr, což je směs kyseliny octové a octanu sodného.

Rovnováhy v tomto pufru můžeme popsat rovnicemi:

CH₃COOH + H₂O ↔ CH₃COO^– + H₃O⁺

CH₃COONa + H₂O ↔ CH₃COOH + Na⁺ + OH^–

Přídavkem kyseliny vzniknou molekuly kyseliny octové, přídavkem zásady ionty octanu. pH roztoku se nezmění.

$$pH = pK_a + \log\frac{[A^-]}{[HA]}$$

$$pH = 14 – pK_b + \log\frac{[B^+]}{[BH]}$$

Pufr	Rozsah pH
Acetátový	3,8 – 5,8
KH₂PO₄	6,2 – 8,2
Borátový	8,25 – 10,25

Výpočet pH slabé kyseliny

Jaké je pH 0,2 M kyseliny octové, pK_a = 4,76?

CH₃COOH ↔ CH₃COO^– + H⁺

K_a = 10^-pK_a = 10^-4,76 = 0,000017

Z rovnice disociace vidíme, že koncentrace octanu a H⁺ budou stejné.

$$K_a = \frac{[CH_3COO^-][H^+]}{[CH_3COOH]} = \frac{x.x}{0,2-x}$$

Dosadíme za K_a a upravíme získaný výraz, čímž dostaneme kvadratickou rovnici:

x² + 0,000017x – 0,0000034 = 0

Kvadratickou rovnici vyřešíme pomocí diskriminantu:

$$x_{1,2} = \frac{-b\pm\sqrt{D}}{2a} = \frac{-b\pm\sqrt{b^2-4ac}}{2a} =
\frac{-0,000017\pm\sqrt{0,000017^2-4 \cdot 1 \cdot (-0,0000034)}}{2 \cdot 1}$$

Ze dvou vypočítaných kořenů zvolíme ten kladný, koncentrace totiž nemůže být záporná.

x = 0,0018

pH = -log[H⁺] = -log0,018 = 2,74

Prezentace ke stažení.

Řešené příklady

Několik řešených příkladů najdete zde.

Další kapitoly

One Reply to “pH, aktivita roztoku”